Importante
A continuación veremos un resumen todo lo visto en esta situación de aprendizaje:
Números reales
Los números que sirven para contar son los naturales: $\mathbb{N}=\{\text{1, 2, 3, 4...}\}$. Algunos autores, también consideran que el $0$ es un número natural, ya que sirve para indicar la ausencia de algo, además de esta forma la suma tendría un elemento neutro.
Al conjunto de los números naturales, se le añaden los negativos y el cero, si es el caso, para obtener el conjunto de los números enteros: $\mathbb{Z}=\{\text{.., -2, -1, 0, 1, 2, ...}\}$
La siguiente ampliación consiste en añadir las fracciones no enteras obteniendo el conjunto de los racionales, $\mathbb{Q}$, en el cual se incluyen todas las fracciones, o lo que es equivalente: todos los enteros, los decimales exactos y los decimales periódicos.
La última ampliación es añadir los números irracionales, $\mathbb{I}$, es decir, los que no se pueden expresar como una fracción, pero que nos lo encontramos en nuestra realidad: $\pi, \sqrt{2}$... o lo que es lo mismo, los números con infinitos decimales no periódicos. Con esta ampliación obtenemos el conjunto de los números reales, $\mathbb{R}$.
Intervalos
Los intervalos son un conjunto de números comprendidos entre dos valores reales, o bien, superiores o inferiores a un número real (semirrecta).
Los extremos pueden estar incluidos (cerrado) o bien excluidos (abiertos).
Existen tres formas de representarlos:
- Mediante paréntesis (abierto) o corchetes (cerrado): $(1,2), (1,2], [1,2), [1,2]$...
- Con desigualdades: $\{x/x>2\}$ o $\{x/1<2\leq3\}$...
- Gráficamente, donde si el punto está incluido se dibuja relleno y si es excluido vacío:
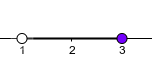
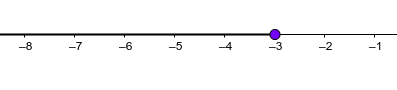
Radicales
Decimos que $\sqrt[n]{a}=b$ si $b^n=a$, en otras palabras, es la operación inversa de la potenciación.
Algunas cuestiones importantes relacionado con una solución dada en radicales:
- Debemos extraer los factores posibles.
- Los radicales iguales hay que sumarlos o restarlos.
- Debemos racionalizar: encontrar una expresión equivalente, sin radicales en el denominador.
Logaritmos
Decimos que $\log_b(a)=c$ si $b^c=a$ con $a$ y $b$ positivos. De nuevo vemos una operación relacionada con la potencia, pero en este caso, lo que buscamos es el exponente.
Los logaritmos de base 10, se llaman decimales y se escriben simplemente $\log a$, es decir, no es necesario indicar la base del logaritmo. Cuando la base del logaritmo es el número $e$, entonces decimos que se trata de un logaritmo neperiano y se escribe $\ln a$ o bien $\text{Ln a}$.
La utilidad de los logaritmos está en sus propiedades, ya que convierten multiplicaciones en sumas, divisiones en restas, potencias en multiplicaciones y radicales en divisiones, lo cual es muy útil para expresiones muy complejas, sobre todo antes de la invención de las calculadoras, de hecho las calculadoras los usan para estos cálculos.
Los humanos usamos una escala logarítmica (en vez de ir de uno en uno, va de 1, 10, 100...) en nuestras percepciones, así por ejemplo, nuestra vista puede detectar la variación de 1 punto a 2 puntos, pero es incapaz de darse cuanta cuando pasas de 1000 puntos a 1001 puntos.